About Z-оrder and R-tree

The index-based Z-order the curve compared to R-tree has a lot of advantages, it:

the

implemented as a normal B-tree, and we know that
B-tree page have the best occupancy rate, in addition,
Z-the keys themselves are more compact
B-tree has a natural order, in contrast to R-tree
B-tree is built faster
B-tree is more balanced
B-tree is clear, is not dependent on heuristics of splitting/merging pages
B-tree does not degrade with constant changes
...

However, the indexes based on Z-order, there is a disadvantage — relatively low performance :). Under the cut we will try to understand what is this fault and can anything to do with it.

Roughly, the meaning of the Z-curve is, we alternate digits are x &y coordinates into a single value as a result. Example — (x = 33 (0001 010), y=22 (01 0110), Z=1577 (0110 0010 1001). If two points close to the coordinates, then most likely the Z - value they will be close.
Three-dimensional (or more) variant is designed the same way we rotate the bits three (or more) coordinates.

And to search in a certain extent we have to “rasterize” all Z values curve for this extent to find a continuous interval in each search.

Here's an illustration for the extent [111000...111000][111400...111400] (675 intervals), the upper-right corner (each continuous zigzag — single spaced):

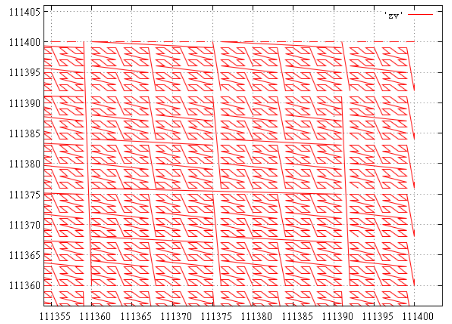
And, for example, to the extent [111000...111000][112000...112000] we get 1688 continuous intervals, obviously, their number mainly depends on the length of the perimeter. Looking ahead, the test data in this extent has got 15 points in 6 intervals.

Yes, most of these small intervals, up to degenerate — of the same value. Nevertheless, even if all this extent just one value, it can be in any of the intervals. And, whether we like it or not, have to do everything 1688 subqueries to find out how many points in fact.

To view all of the value of the lower left corner to upper right is not an option, the difference between the angles in this case — 3 144 768, we'll have to see in three times more data and this is not the worst case. For example, the extent of the [499500...499500][500500...500500] will give the range of 135 263 808 values in ~135 times larger than the area of the extent.

And then we can ask the traditional question —

the

what if ...

Suppose we do an empty index, really, to do all those hundreds and thousands of subqueries to understand it? No, only one from the lower left to the upper right.

Now suppose that the extent is small enough and the data are sparse and likely to find something a little. Let's execute the same query from corner to corner. If nothing was found, so nothing there. Otherwise, there is a chance. But as we have seen, the area covered by the query from corner to corner many times can exceed the extent of the search and we have no desire to read is obviously junk data. Therefore, we will not view the entire cursor, and take from it only the minimum Z-value. To do this, the query is performed (order by) and (top 1).

So we have some value. For example, this value is not from the extent that it can give? It's time to remember that we have a sorted array a [1...N] of the ranges of the subqueries. We perform binary search and find out what subqueries squeezed this value, though, between m and m+1. Great, so the requests from 1 to m, can not carry, there's obviously nothing there.

If the value belongs to our extent, so it falls into one of our ranges and we can also find in some, suppose, too, m. As before, the queries with numbers 1 ... m-1 are not required. But the interval m deserves a separate query that will give us all that it is.
What perhaps is more data, continue. Again execute the query, but not from corner to corner, and from the beginning of the interval m+1 to the top right corner. And will continue to do so until we reach the end of the list of intervals.

That's the whole idea, note it works fine in the case when the extent of the plenty or even lots of data. At first glance, this will drastically reduce the number of queries and speed up work.

It's time to test the idea in practice. As a test platform we use PostgeSQL 9.6.1, GiST. The measurements were carried out on a modest virtual machine with two cores and 4 GB of RAM, so the times are not absolute values, but the numbers of pages read can be trusted.

the

Original data

As the data used by 100 million random points in the extent [0...1 000 000][0...1 000 000].

Get a table for 2-dimensional point data:

the

create table test_points (x integer,y integer);

Data create:

gawk script

BEGIN{
for (i = 0; i < 100000000; i++)
{
x = int(1000000 * rand());
y = int(1000000 * rand());
print x"\t"z;
}
exit(0);
}

Sort the resulting file (explanation later) and the COPY operator fill it to the table:

the

COPY test_points from '/home/.../data.csv';

Fill in the table takes a few minutes. The size of the data (\dt+) — 4358 Mb

the

R-tree

The corresponding index is created with the command:

the

create index test_gist_idx on test_points using gist ((point(x,y)));

But there is a caveat. On random data the index is very long (at least the author wasn't time to line up for the night). Building on pre-sorted data took about an hour.

The size of the index (\di+) — 9031 Mb

In fact, for us the order of the data in the table is not important but it needs to be shared between different methods, so I had to use a sorted table.

A test query looks like this:

the

select count(1) from test_points where 
point(x,y) < @ box(point("xmin","ymin"),point("xmax","ymax"));

the

Check for normal indices

To verify that will perform spatial queries on separate indexes for x &y. They are made so:

the

create index x_test_points on test_points (x);
create index y_test_points on test_points (y);

It takes a few minutes.

Test query:

the

select count(1) from test_points where 
x >= "xmin" and x <= "xmax" and y >= "ymin" and y <= "ymax";

the

Z-index

Now we need a function able to convert x,y coordinates in Z-value.

Start to create extension, function in it:

the

CREATE FUNCTION zcurve_val_from_xy(bigint, bigint) RETURNS bigint
AS 'MODULE_PATHNAME'
LANGUAGE C IMMUTABLE STRICT;

the body:

static uint32 stoBits[8] = {0x0001, 0x0002, 0x0004, 0x0008, 
0x0010, 0x0020, 0x0040, 0x0080};
uint64
zcurve_fromXY (uint32 ix, iy uint32)
{
uint64 val = 0;
int curmask = 0xf;
unsigned char *ptr = (unsigned char *)&val;
int i;
for (i = 0; i < 8; i++)
{
int xp = (ix & curmask) >> (i<<2);
int yp = (FP & curmask) >> (i<<2);
int tmp = (xp & stoBits[0]) | ((yp & stoBits[0])<<1) |
((xp & stoBits[1])<<1) | ((yp & stoBits[1])<<2) |
((xp & stoBits[2])<<2) | ((yp & stoBits[2])<<3) |
((xp & stoBits[3])<<3) | ((yp & stoBits[3])<<4);
curmask <<= 4;
ptr[i] = (unsigned char)tmp;
}
return val;
}
Datum
zcurve_val_from_xy(PG_FUNCTION_ARGS)
{
uint64 v1 = PG_GETARG_INT64(0);
uint64 v2 = PG_GETARG_INT64(1);
PG_RETURN_INT64(zcurve_fromXY(v1, v2));
}

Now (after CREATE EXTENSION, of course) Z-index is as follows:

the

create index zcurve_test_points on test_points(zcurve_val_from_xy(x, y));

It takes a few minutes (and does not require sorting of the data).

The size of the index (\di+) — 2142 Mb (~4 times less than the R-tree)

the

Search a to Z index

So, in our first (let's call it “naive”) version, we will do so:

To the extent of size dx*dy we make an array of the IDs of the appropriate size
For each point in the extent vechicles Z value
Sort the array of IDs

For each interval perform a subquery of the form:

the

select * from test_points where zcurve_val_from_xy(x, y) between $1 and $2

Get the result

To search using this option will use the function (body below):

the

CREATE FUNCTION zcurve_oids_by_extent(bigint, bigint, bigint, bigint)
RETURNS bigint
AS 'MODULE_PATHNAME'
LANGUAGE C IMMUTABLE STRICT;

Spatial query using this function looks like this:

the

select zcurve_oids_by_extent("xmin","ymin","xmax","ymax") as count;

The function returns only the number of hits, the data can optionally be output using the “elog(INFO,...)”.

Second, superior, (let's call it “sample”) option as follows:

to the extent of size dx*dy we make an array of the IDs of the appropriate size
for each point in the extent vechicles Z value
sort the array of IDs
find continuous time intervals
starting with the first occurrence of the interval:
1. Execute “test” query type (the parameters — the boundaries of the interval):
  
  the
```
select * from test_points where 
zcurve_val_from_xy(x, y) between $1 and $2 
order by zcurve_val_from_xy(x, y) limit 1
```
2. If the query found nothing, and then the data in the search extent is not left out.
3. Now we can perform the found Z-value:
  1. Look, was it any of our intervals.
  2. If not, find the next rest interval and go to item 5.
  3. If hit, perform a query for the interval type:
    
    the
```
select * from test_points 
where zcurve_val_from_xy(x, y) between $1 and $2
```
  4. Take the next interval and go to item 5.

To search using this option will use the function:

the

CREATE FUNCTION zcurve_oids_by_extent_ii(bigint, bigint, bigint, bigint)
RETURNS bigint
AS 'MODULE_PATHNAME'
LANGUAGE C IMMUTABLE STRICT;

Spatial query using this function looks like this:

the

select zcurve_oids_by_extent_ii("xmin","ymin","xmax","ymax") as count;

The function returns only the number of hits.

the

Rendering

In the described algorithms used a very simple and inefficient algorithm “rasterization” — get a list of intervals.

On the other hand, it is easy to perform the measurements of average times of his work on random extents of the desired size. Here they are:
the the the the the the

Extent dx * dy	Expected average number of points in the results	Time, MS
100X100	1	.96 (.37 + .59)
316X316	10	11 (3.9 + 7.1)
1000X1000	100	119.7 (35 + 84.7)
3162X3162	1000	1298 (388 + 910)
10000X10000	10 000	14696 (3883 + 10813)

In the parentheses are shown separately for two phases — the calculation of Z values and sorting

the

Results

Here's a summary table.
the the the the the the

Npoints	Type	Time(ms)	Reads	Shared Hits
1	X&Y rtree Z-value Z-value-ii	43.6 .5 8.3(9.4) 1.1(2.2)	59.0173 4.2314 4.0988 4.1984 (12.623)	6.1596 2.6565 803.171 20.1893 (57.775)
10	X&Y rtree Z-value Z-value-ii	83.5 .6 15(26) 4(15)	182.592 13.7341 14.834 14.832 (31.439)	9.24363 2.72466 2527.56 61.814 (186.314)
100	X&Y rtree Z-value Z-value-ii	220 2.1 80(200) 10(130)	704.208 95.8179 95.215 96.198 (160.443)	16.528 5.3754 8007.3 208.214 (600.049)
1000	X&Y rtree Z-value Z-value-ii	740 12 500(1800) 200(1500)	3176.06 746.617 739.32 739.58 (912.631)	55.135 25.439 25816 842.88 (2028.81)
10 000	X&Y rtree Z-value Z-value-ii	2 500 1 70 ... 200 4700(19000) 1300(16000)	12393.2 4385.64 4284.45 4305.78 (4669)	101.43 121.56 86274.9 5785.06 (9188)

Npoints — the average number of points in the results.

Type -

‘X&Y’ — the use of separate indexes for x & y
‘rtree’ query using R-tree
‘Z-value-ii’ — search intervals with samples

Time(ms) — average time of query execution. Under these conditions, the value is very unstable, depends on the DBMS cache and the disk cache of the virtual machine from the disk cache of the host system. Here are more for reference. For Z-value and Z-value-ii given 2 numbers. In parenthesis is the actual time. Without the brackets — time for less costs “rasterization”.

Reads — the average number of reads per request (received via EXPLAIN (ANALYZE,BUFFERS))

Shared hits — the number of accesses to buffers (...)
For Z-value-ii column Reads & Shared hits given 2 numbers. In parentheses is the total number of readings. Without the parentheses — less probing queries with order by and limit 1. This is done because of the opinion that such a request reads all data in the interval, sorts and gives the minimum, instead of just give 1 value of the already sorted index. Therefore, statistics on such requests were considered unnecessary, but is included for reference.

The times shown in the second runs, on a heated server and virtual machine. The number of read buffers — into the fresh-raised server.

All queries were read and the data of the table not belonging to the indexes. However, this same data to the same table, so for all types of queries we obtained a constant value.

the

Insights

R-tree is still very good in statics, the efficiency of page reads is very high.
But a Z-order index sometimes have to read pages that no need. This occurs when testing the cursor falls between intervals, it is likely that this gap will be a lot of people's points and specific page does not contain any totals.

however, due to more dense packing of the Z-order is close to the R-tree for the real number of pages read. This suggests that the potentially Z-order is capable of delivering close performance.
the

Z-order index is reading huge number of pages from the cache because many times requests are made at the same place. On the other hand, these readings are relatively inexpensive.
For large queries, the Z-order loses much speed on the R-tree. The reason is that to run subqueries, we use SPI is the top level and not too fast engine. And with the “rasterization” of course, it is necessary to do something.
At first glance, the use of sampling intervals is not much that speeds up the work, and formally even worsened statistics page reads. But we must understand that it costs a high-level means that we had to use. Potentially the index based on Z-order is not worse than R-tree in performance and much better on other performance characteristics.

the

Perspectives

To create the Z-order curve full-fledged spatial index, which would be able to compete with R-tree, it is necessary to solve the following problems:

the

to come up with an inexpensive algorithm to obtain a list of pointervalue to the extent
switch to low-level access to tree index

Fortunately, both is not something impossible.

Source

#include "postgres.h"
#include "catalog/pg_type.h"
#include "fmgr.h"
#include <string.h>
#include "executor/spi.h"

PG_MODULE_MAGIC;

zcurve_fromXY uint64 (uint32 ix, iy uint32);
void zcurve_toXY (al uint64, uint32 *RX, uint32 *py);

static uint32 stoBits[8] = {0x0001, 0x0002, 0x0004, 0x0008, 
0x0010, 0x0020, 0x0040, 0x0080};
uint64
zcurve_fromXY (uint32 ix, iy uint32)
{
uint64 val = 0;
int curmask = 0xf;
unsigned char *ptr = (unsigned char *)&val;
int i;
for (i = 0; i < 8; i++)
{
int xp = (ix & curmask) >> (i<<2);
int yp = (FP & curmask) >> (i<<2);
int tmp = (xp & stoBits[0]) | ((yp & stoBits[0])<<1) |
((xp & stoBits[1])<<1) | ((yp & stoBits[1])<<2) |
((xp & stoBits[2])<<2) | ((yp & stoBits[2])<<3) |
((xp & stoBits[3])<<3) | ((yp & stoBits[3])<<4);
curmask <<= 4;
ptr[i] = (unsigned char)tmp;
}
return val;
}

void 
zcurve_toXY (al uint64, uint32 *RX, uint32 *py)
{
unsigned char *ptr = (unsigned char *)&al;

int iy = 0;
int i;

if (!px || !py)
return;

for (i = 0; i < 8; i++)
{
int tmp = ptr[i];
int tmpx = (tmp & stoBits[0]) + ((tmp & stoBits[2])>>1) + ((tmp & stoBits[4])>>2) + ((tmp & stoBits[6])>>3);
int tmpy = ((tmp & stoBits[1])>>1) + ((tmp & stoBits[3])>>2) + ((tmp & stoBits[5])>>3) + ((tmp & stoBits[7])>>4);
ix |= tmpx << (i << 2);
iy |= tmpy << (i << 2);
} 
*px = ix;
*py = iy;
}

PG_FUNCTION_INFO_V1(zcurve_val_from_xy);

Datum
zcurve_val_from_xy(PG_FUNCTION_ARGS)
{
uint64 v1 = PG_GETARG_INT64(0);
uint64 v2 = PG_GETARG_INT64(1);

PG_RETURN_INT64(zcurve_fromXY(v1, v2));
}


static const int s_maxx = 1000000;
static const int s_maxy = 1000000;

#ifndef MIN
#define MIN(a,b) ((a) < (b)?(a):(b))
#endif


static int compare_uint64( const void *arg1, const void *arg2 )
{
const uint64 *a = (const uint64 *)arg1;
const uint64 *b = (const uint64 *)arg2;
if (*a == *b)
return 0;
return *a > *b ? 1: -1;
}

SPIPlanPtr prep_interval_request();
int fin_interval_request(SPIPlanPtr pplan);
int run_interval_request(SPIPlanPtr pplan, v0 uint64, uint64 v1);

SPIPlanPtr prep_interval_request()
{
SPIPlanPtr pplan;
char sql[8192];
int nkeys = 2;
Oid argtypes[2] = {INT8OID, INT8OID}; /* key types to prepare execution plan */
int ret =0;

if ((ret = SPI_connect()) < 0)
/* internal error */
elog(ERROR, "check_primary_key: SPI_connect returned %d", ret);

snprintf(sql, sizeof(sql), "select * from test_points where zcurve_val_from_xy(x, y) between $1 and $2");

/* Prepare plan for query */
pplan = SPI_prepare(sql, nkeys, argtypes);
if (pplan == NULL)
/* internal error */
elog(ERROR, "check_primary_key: SPI_prepare returned %d", SPI_result);
return pplan;
}

int fin_interval_request(SPIPlanPtr pplan)
{
SPI_finish();
return 0;
}


int 
run_interval_request(SPIPlanPtr pplan, v0 uint64, uint64 v1)
{
Datum values[2]; /* key types to prepare execution plan */
Portal portal;
int cnt = 0, i;

values[0] = Int64GetDatum(v0);
values[1] = Int64GetDatum(v1);

portal = SPI_cursor_open(NULL, pplan, values, NULL, true);
if (NULL == portal)
/* internal error */
elog(ERROR, "check_primary_key: SPI_cursor_open");
for (;;)
{
SPI_cursor_fetch(portal, true, 8);
if (0 == SPI_processed || NULL == SPI_tuptable)
break;
{
TupleDesc tupdesc = SPI_tuptable- > tupdesc;
for (i = 0; i < SPI_processed; i++)
{
HeapTuple tuple = SPI_tuptable- > vals[i];
//elog(INFO, "%s, %s", SPI_getvalue(tuple, tupdesc, 1), SPI_getvalue(tuple, tupdesc, 2));
cnt++;
}
}
}
SPI_cursor_close(portal);

return cnt;
}

PG_FUNCTION_INFO_V1(zcurve_oids_by_extent);
Datum
zcurve_oids_by_extent(PG_FUNCTION_ARGS)
{
SPIPlanPtr pplan;

uint64 x0 = PG_GETARG_INT64(0);
uint64 y0 = PG_GETARG_INT64(1);
uint64 x1 = PG_GETARG_INT64(2);
uint64 y1 = PG_GETARG_INT64(3);
uint64 *ids = NULL;
int cnt = 0;
int sz = 0, ix, iy;

x0 = MIN(x0, s_maxx);
y0 = MIN(y0, s_maxy);
x1 = MIN(x1, s_maxx);
y1 = MIN(y1, s_maxy);

if (x0 > x1)
elog(ERROR, "xmin > xmax");
if (y0 > y1)
elog(ERROR, "ymin > ymax");

sz = (x1 - x0 + 1) * (y1 - y0 + 1);
ids = (uint64*)palloc(sz * sizeof(uint64));
if (NULL == ids)
/* internal error */
elog(ERROR, "cant alloc %d bytes in zcurve_oids_by_extent", sz);
for (ix = x0; ix <= x1; ix++)
for (iy = y0; iy < = y1;++iy)
{
ids[cnt++] = zcurve_fromXY(ix, iy);
}
qsort (ids, sz, sizeof(*ids), compare_uint64);

cnt = 0;

pplan = prep_interval_request();
{
// FILE *fl = fopen("/tmp/ttt.sql", "w");
int cur_start = 0; 
int ix;
for (ix = cur_start + 1; ix < sz; ix++)
{
if (ids[ix] != ids[ix - 1] + 1)
{
cnt += run_interval_request(pplan, ids[cur_start], ids[ix - 1]);
// fprintf(fl, "EXPLAIN (ANALYZE,BUFFERS) select * from test_points where zcurve_val_from_xy(x, y) between %ld and %ld;\n", ids[cur_start], ids[ix - 1]);
// elog(INFO, "%d - > %d (%ld - > %ld)", cur_start, ix - 1, ids[cur_start], ids[ix - 1]);
// cnt++;
cur_start = ix;
}
}
if (cur_start != ix)
{
cnt += run_interval_request(pplan, ids[cur_start], ids[ix - 1]);
// fprintf(fl, "EXPLAIN (ANALYZE,BUFFERS) select * from test_points where zcurve_val_from_xy(x, y) between %ld and %ld;\n", ids[cur_start], ids[ix - 1]);
// elog(INFO, "%d - > %d (%ld - > %ld)", cur_start, ix - 1, ids[cur_start], ids[ix - 1]);
}
// fclose(fl);
}
fin_interval_request(pplan);
pfree(ids);

PG_RETURN_INT64(cnt);
}

//------------------------------------------------------------------------------------------------

interval_ctx_s struct {
SPIPlanPtr cr_;
SPIPlanPtr probe_cr_;
uint64 cur_val_;
uint64 top_val_;
FILE * fl_;
};
typedef struct interval_ctx_s interval_ctx_t;

int prep_interval_request_ii(interval_ctx_t *ctx);
int run_interval_request_ii(interval_ctx_t *ctx, uint64 v0, v1, uint64);
int probe_interval_request_ii(interval_ctx_t *ctx, uint64 v0);
int fin_interval_request_ii(interval_ctx_t *ctx);


int prep_interval_request_ii(interval_ctx_t *ctx)
{
char sql[8192];
int nkeys = 2;
Oid argtypes[2] = {INT8OID, INT8OID}; /* key types to prepare execution plan */
int ret =0;

if ((ret = SPI_connect()) < 0)
/* internal error */
elog(ERROR, "check_primary_key: SPI_connect returned %d", ret);

snprintf(sql, sizeof(sql), "select * from test_points where zcurve_val_from_xy(x, y) between $1 and $2");
ctx->cr_ = SPI_prepare(sql, nkeys, argtypes);
if (ctx->cr_ == NULL)
/* internal error */
elog(ERROR, "check_primary_key: SPI_prepare returned %d", SPI_result);

snprintf(sql, sizeof(sql), "select * from test_points where zcurve_val_from_xy(x, y) between $1 and %ld order by zcurve_val_from_xy(x::int4, y::int4) limit 1", ctx->top_val_);
ctx->probe_cr_ = SPI_prepare(sql, 1, argtypes);
if (ctx->probe_cr_ == NULL)
/* internal error */
elog(ERROR, "check_primary_key: SPI_prepare returned %d", SPI_result);

return 1;
}

int 
probe_interval_request_ii(interval_ctx_t *ctx, uint64 v0)
{
Datum values[1]; /* key types to prepare execution plan */
Portal portal;

values[0] = Int64GetDatum(v0);
{
// uint32 lx, ly;
// zcurve_toXY (v0, &lx, &ly);
//
// elog(INFO, "probe(%ld:%d,%d)", v0, lx, ly);
}

if (ctx->fl_)
fprintf(ctx->fl_, "EXPLAIN (ANALYZE,BUFFERS) select * from test_points where zcurve_val_from_xy(x, y) between %ld and %ld order by zcurve_val_from_xy(x::int4, y::int4) limit 1;\n", v0, ctx->top_val_);
portal = SPI_cursor_open(NULL, ctx->probe_cr_, values, NULL, true);
if (NULL == portal)
/* internal error */
elog(ERROR, "check_primary_key: SPI_cursor_open");
{
SPI_cursor_fetch(portal, true, 1);
if (0 != SPI_processed && NULL != SPI_tuptable)
{
TupleDesc tupdesc = SPI_tuptable- > tupdesc;

bool isnull;
HeapTuple tuple = SPI_tuptable- > vals[0];
Datum dx, dy;
uint64 CL = 0;
dx = SPI_getbinval(tuple, tupdesc, 1, &isnull);
dy = SPI_getbinval(tuple, tupdesc, 2, &isnull);
CL = zcurve_fromXY(DatumGetInt64(dx), DatumGetInt64(dy));
// elog(INFO, "%ld %ld - > %ld", DatumGetInt64(dx), DatumGetInt64(dy), CL);

ctx->cur_val_ = zv;
SPI_cursor_close(portal);
return 1;
}
SPI_cursor_close(portal);
}
return 0;
}


int 
run_interval_request_ii(interval_ctx_t *ctx, v0 uint64, uint64 v1)
{
Datum values[2]; /* key types to prepare execution plan */
Portal portal;
int cnt = 0, i;

values[0] = Int64GetDatum(v0);
values[1] = Int64GetDatum(v1);
// elog(INFO, "[%ld %ld]", v0, v1);

if (ctx->fl_)
fprintf(ctx->fl_, "EXPLAIN (ANALYZE,BUFFERS) select * from test_points where zcurve_val_from_xy(x, y) between %ld and %ld;\n", v0, v1);
portal = SPI_cursor_open(NULL, ctx->cr_, values, NULL, true);
if (NULL == portal)
/* internal error */
elog(ERROR, "check_primary_key: SPI_cursor_open");
for (;;)
{
SPI_cursor_fetch(portal, true, 8);
if (0 == SPI_processed || NULL == SPI_tuptable)
break;
{
TupleDesc tupdesc = SPI_tuptable- > tupdesc;
for (i = 0; i < SPI_processed; i++)
{
HeapTuple tuple = SPI_tuptable- > vals[i];
// elog(INFO, "%s, %s", SPI_getvalue(tuple, tupdesc, 1), SPI_getvalue(tuple, tupdesc, 2));
cnt++;
}
}
}
SPI_cursor_close(portal);

return cnt;
}


PG_FUNCTION_INFO_V1(zcurve_oids_by_extent_ii);
Datum
zcurve_oids_by_extent_ii(PG_FUNCTION_ARGS)
{
uint64 x0 = PG_GETARG_INT64(0);
uint64 y0 = PG_GETARG_INT64(1);
uint64 x1 = PG_GETARG_INT64(2);
uint64 y1 = PG_GETARG_INT64(3);
uint64 *ids = NULL;
int cnt = 0;
int sz = 0, ix, iy;
interval_ctx_t ctx;

x0 = MIN(x0, s_maxx);
y0 = MIN(y0, s_maxy);
x1 = MIN(x1, s_maxx);
y1 = MIN(y1, s_maxy);

if (x0 > x1)
elog(ERROR, "xmin > xmax");
if (y0 > y1)
elog(ERROR, "ymin > ymax");

sz = (x1 - x0 + 1) * (y1 - y0 + 1);
ids = (uint64*)palloc(sz * sizeof(uint64));
if (NULL == ids)
/* internal error */
elog(ERROR, "can't alloc %d bytes in zcurve_oids_by_extent_ii", sz);
for (ix = x0; ix <= x1; ix++)
for (iy = y0; iy < = y1;++iy)
{
ids[cnt++] = zcurve_fromXY(ix, iy);
}
qsort (ids, sz, sizeof(*ids), compare_uint64);

ctx.top_val_ = ids[sz - 1];
ctx.cur_val_ = 0;
ctx.cr_ = NULL;
ctx.probe_cr_ = NULL;
ctx.fl_ = NULL;//fopen("/tmp/ttt.sql", "w");

cnt = 0;

prep_interval_request_ii(&ctx);
{
int cur_start = 0; 
int ix;
for (ix = cur_start + 1; ix < sz; ix++)
{
if (0 == probe_interval_request_ii(&ctx, ids[cur_start]))
break;
for (; cur_start < sz && ids[cur_start] < ctx.cur_val_; cur_start++);
// if (ctx.cur_val_ != ids[cur_start])
// {
// cur_start++;
// continue;
// }
ix = cur_start + 1;
if (ix > = sz)
break;
for (; ix < sz && ids[ix] == ids[ix - 1] + 1; ix++);
//elog(INFO, "%d %d %d", ix, cur_start, sz);
cnt += run_interval_request_ii(&ctx, ids[cur_start], ids[ix - 1]);
cur_start = ix;
}
}
if (ctx.fl_)
fclose(ctx.fl_);
fin_interval_request(NULL);
pfree(ids);

PG_RETURN_INT64(cnt);
}

Post here, and not posted on github because the code is purely experimental and has no practical value.

PPS: a Huge thanks to the guys from PostgresPro for what inspired me to this work.

P. p. p. S.: continuation here and here

Article based on information from habrahabr.ru

Поиск по этому блогу

computer express